The minimum FFT size (2^N) set in the Wave GUI plays a crucial role in relation to how the M21 MA engine processes the wave data.
Unlike all other MIKE 21 models, the M21 MA engine does not simply interpolate the wave data to each computational time step in the simulation period, during the simulation.
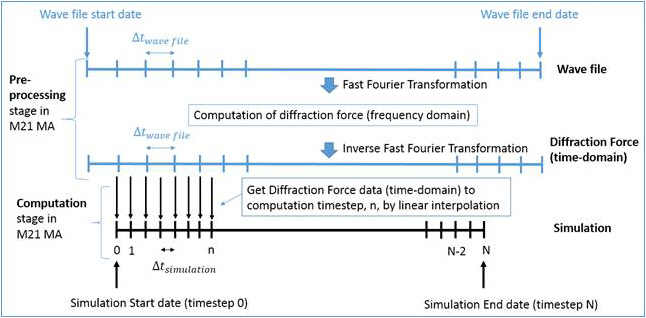
Instead the wave data plays an implicit role in the computation, as it is the foundation for the computation of the diffraction forces the vessel hull is exposed to due to the wave induced pressure. The engine interpolates the computed diffraction force to each computational time step, see Figure 1.9.

Figure 1.9 Description of interpolation process
The computation of diffraction forces on the vessel hull takes place in the frequency domain, through usage of FFT and the IFFT (Inverse Fast Fourier Transformation) algorithms.
In signal processing terms, the wave file thus represents the available full sample (of wave steps), which the FFT can resolve into a discrete spectrum of frequency bins. The more points (wave steps) included in the FFT, the more frequency bins will be available to identify the frequency spectrum of the sample.
The precision/quality of the wave forcing computation on the vessel hull (diffraction force), will thus strongly depend on how many wave steps are included in the FFT.
The Min. FFT size (2^N) on the Waves GUI grants the user a tool for controlling how many Wave steps are to be processed in FFT/IFFT. It has the interpretation:
The minimum number of steps from the wave file, covering the simulation period, required to resolve all the wave frequencies and be processed in the FFT/IFFT.
The M21 MA engine identifies the specific wave steps to be FFT/IFFT processed using the following steps:
1. Find the largest interval of 2^N wave steps covering the simulation period ≥ Min. FFT Size (2^N)
2. If the interval is found
=> process this 2^N wave step interval in FFT/IFFT
3. If no such interval is found
=> Zero-pad the full set of wave steps from the wave file up to nearest 2^N size
=> process this (artificially increased) 2^N step interval in FFT/IFFT
How to set the Min. FFT Size (2^N) will depend on the individual case. There are two possibilities, which are presented in the following.
Case 1: Simulation period and wave file period are identical or almost identical
Given that the wave file contains sufficiently many steps to resolve the waves full frequency content by FFT/IFFT (general recommendation of minimum wave steps is 4096), then the Min. FFT Size (2^N) will not play a role here.
Because the simulation and the wave covers the same time axis extent, the engine will use a sufficient amount of wave steps for FFT/IFFT (regardless of how they're identified), hence the diffraction forces used in the simulation will be computed as precise as possible. This case is illustrated in Figure 1.10.

Figure 1.10 Illustration of interpolation for Case 1
Recommendation: no attention needs to be paid to the Min. FFT Size (2^N).
Case 2: Short simulation with long wave file period
It is in cases like these where the Min. FFT Size (2^N) will be most relevant to apply.
Here the simulation duration is small, but in order to produce diffraction force data for the simulation timesteps of sufficient quality (include enough steps for FFT/IFFT), many more wave steps than what just covers the simulation period is needed to be processed.
Here a sufficiently high Min. FFT Size (2^N) will help ensure that enough wave steps will be processed in FFT/IFFT for the diffraction forces to be computed with appropriate accuracy. This case is illustrated in Figure 1.11.
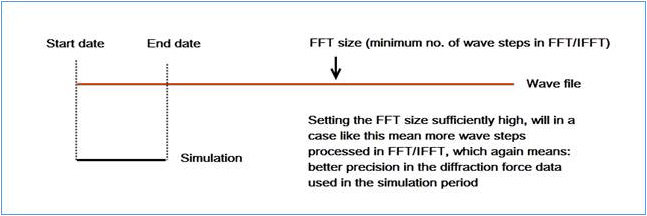
Figure 1.11 Illustration of interpolation for Case 2
Recommendation: In order for the FFT to capture enough of the waves frequency content, it must be assessed if enough wave steps cover the simulation period. If this is not the case, then the Min. FFT Size (2^N) should be increased to a value assessed to be high enough to capture enough frequency content (the general recommendation of minimum number of wave steps is 4096).