Bijker's Transport Method

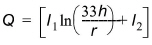
According to Bijker, the total-load sediment transport, q_t, is calculated as the sum of bed-load transport, q_b, and suspended load transport, q_s.

qt = qb + qs = qb(1 + 1.83Q)

Q is a dimensionless factor defined as

(5.7)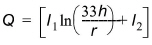   

where h is the water depth, r is the bed roughness and I₁ and I₂ are Einstein's integrals, which must be evaluated numerically on the basis of the dimension­less reference level A = r/h and z*, defined as:

(5.8)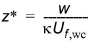   

w is the settling velocity of the suspended sediment, k is von Karman's con­stant and U_f,wc is the shear velocity under combined waves and current. The influence of the waves on the suspended-load transport is therefore taken into account through the shear velocity, U_f,wc.

The roughness, r, can be related to the Chezy number, C, through

(5.9)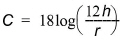   

Following Bijker, the shear velocity in combined waves and current U_f,wc is found as

(5.10)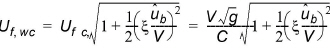   

where U_f,c is the current-related shear velocity, V is the depth-averaged cur­rent velocity, û_b is the amplitude of the wave-induced oscillatory velocity at the bottom, and x is a dimensionless factor that can be expressed in terms of the wave friction factor f_w and Chezy's number C.

(5.11)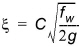   

The wave friction factor f_w is calculated according to Swart as

(5.12)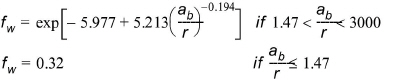   

a_b is the amplitude of the wave motion at the bottom.

(5.13)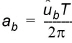   

a_b and û_b are evaluated using linear wave theory.

The bed load transport, q_b, and suspended load transport, q_s, are calculated according to

(5.14)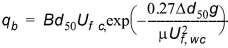   

It is interesting to note that the influence of the waves on the bed-load trans­port, q_b, is accounted for through a "stirring term", i.e. the exponential in the previous equation. The "transporting term" is only related to the current by way of U_f,c. B is a dimensionless bed load transport coefficient, D is the rela­tive density of sediments and m is the so-called "ripple factor". D and m are defined as

(5.15)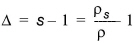   

(5.16)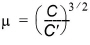   

r_s is the density of the sediment, r is the density of water and C' is the Chezy number related to the geometric characteristics of the bed material. It is cal­culated as

(5.17)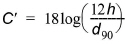   

d₉₀ is the sediment size for which 90% (in weight) of the bed material is finer. For uniform bed material d₉₀ becomes identical to the specified value of d₅₀.