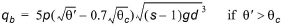
Engelund & Fredsøe Transport Theory

The total-load transport rate q_t is calculated as the sum of the bed-load trans­port q_b and the suspended-load transport rate q_s

q_t = q_b + q_s

It is assumed that bed-load transport takes place in one single layer of thick­ness equal to one grain diameter d. The bed-load transport q_b is calculated as

(5.18)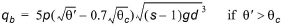   

where p is the probability that all particles in a single layer will be in motion, q’ is the dimensionless bed shear stress (Shields parameter) related to skin fric­tion and q_c is the critical bed shear stress for initiation of motion. s is the rela­tive density of the bed material.

q’ is defined as

(5.19)   

p is defined as

(5.20)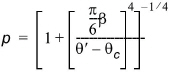   

with b = the dynamic friction coefficient.

Following the ideas of Einstein (1950), the suspended load q_s is evaluated as

(5.21)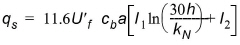   

with c_b = the bed concentration of suspended sediment, U_f’ = the shear veloc­ity related to skin friction, a = 2d = the reference level for c_b, I₁ and I₂ = Ein­stein’s integrals, h = the water depth and k_N = Nikuradse’s equivalent roughness = 2.5d.

The integrals I₁ and I₂ are a function of the dimensionless reference level A = a/h and of the Rouse number z = w_s/kU_f, where w_s is the settling velocity of the suspended sediment and k = von Karman’s constant (»0.40). I₁ and I₂ are integrated between y = a and y = h, where y is measured upwards from the fixed bed level.

Engelund and Fredsøe developed a semi-empirical relation for the value of c_b at a = 2d

(5.22)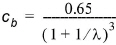   

where the linear concentration l is given by

(5.23)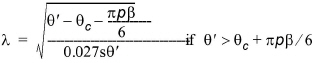   

Note that the transport formulation of Engelund & Fredsøe was developed on the basis of data obtained from experiments with bed material of sand-frac­tion size. Therefore, you should make sure that the bed material used as input to the model falls within the proper range of grain sizes.