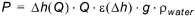
MIKE HYDRO calculates the hydroelectric power produced from the following formula:
Where P is the power generated,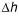 
is the effective head (difference) [L], Q is the discharge/release through turbine(s) [L3/T], 
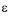is the machine (power) efficiency [-], g is the gravitational constant [L/T2] and 
is the density of water [M/L3]. Machine (power) efficiency 
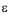may also be specified as a function of Q, in which case 
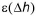is replaced by 
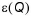in equation (A.2.1).
The effective head difference is:
The hydropower formula is non-linear because of the dependencies of head difference on discharge and machine efficiency. Tailwater levels are generally a function of discharge, and so are additional conveyance head losses in the channel (both increase with discharge). In addition the tailwater can also become governed by backwater from the reservoir downstream rather than discharge of the supplying reservoir. In the simulations, the applicable tailwater level for use in equation (A.2.2) is found from
(A.2.3)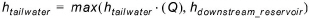 
In MIKE HYDRO, the following inter-dependencies between variables can be assumed constant or insignificant by leaving out the respective detailed specifications:
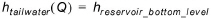(leaving out the tail water table)
(leaving out the conveyance head loss table)
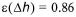(leaving out the power efficiency table)
Water demand for power generation is calculated by solving the power formula, equation (A.2.1), for Q (the solution must be found iteratively). When the effective head difference is small, turbines are however shut off, both because they are inefficient and because the required discharge would grows very large. Accordingly, a minimum head for operation can also be specified. If the head is less than the minimum head, Q is set to zero, i.e., no water is routed through the turbines, regardless of demand.
