When global ranking is activated, all supply connections in the model setup automatically appear in the global ranking dialogue, and each supply connection must be assigned a unique ranking number. The following overall conditions apply to the global ranking feature:
· Ranking numbers are float numbers
· Ranking priority decreases with increasing ranking numbers.
That is, the supply connection with ranking number 1 has first priority, the supply connection with ranking number 2 has second priority, and so on.
· A ranking number is unique. Ranking numbers cannot be shared and each supply connection must have a unique ranking number.
· For Water users with more than 1 supply connection, consecutive ranking numbers should be assigned to ensure consistent priority.
· All supply connections must be assigned a ranking number.
· Only Reservoirs with defined Guide curve levels (pg. 152) will release water to fulfil demands.
Ranking numbers may be displayed in Map view by selecting ‘GlobalPriority’ in the label field for supply connections (in the Symbology tree).
The Global Ranking algorithm
The global ranking allocation algorithm allocates water during each time step as follows:
· First, the algorithm estimates uncontrolled available water at all locations in the model. This includes runoff from catchments, as well as minimum releases from reservoirs and bifurcated water flows.
· Then, unallocated water is allocated by priority order given physical flow constraints until no more unallocated water is left.
This procedure is executed for every time step of the MIKE HYDRO simulation.
When using the global ranking algorithm, users should be aware of how the algorithm handles return flows, bifurcations, and reservoirs.
Return flows
During the allocation process, return flows are estimated and added to the unallocated supply available to downstream users. However, return flows are estimated sequentially as the algorithm moves through the ranking list. Therefore, if a user is located upstream of a downstream user with higher priority, the upstream user's return flow is not included in the available supply to the downstream user. In some cases, this means that a downstream user can cause an unnecessary shortage upstream because the supply available to the downstream user is underestimated.
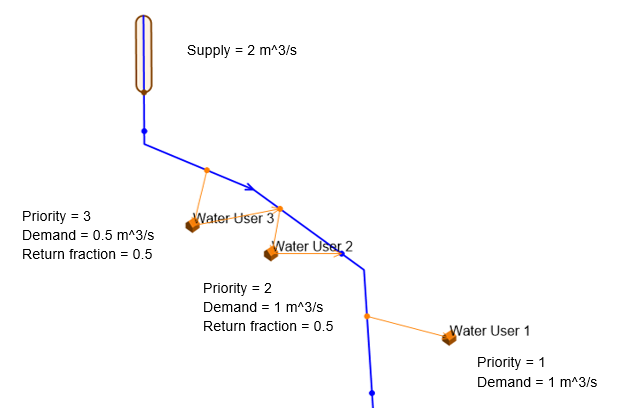
Consider the example in Figure 11.1. In the example, the total supply available is 2 m^3/s and the net demand is 1.75 m^3/s (1 m^3/s + 0.5*1 m^3/s + 0.5*0.5 m^3/s). Therefore, supplies should be sufficient to meet demands.

Figure 11.1 Return Flow example
However, the global ranking algorithm will not allocate any water to Water User 3 in this example. This is because Water User 3 has the lowest priority of the three and is also the most upstream location. The water allocation sequence therefore does not consider a return flow from Water User 2 as part of the available supply to Water User 1, nor a return flow from Water User 3 as part of the available supply to water users 1 and 2. If the priority sequence is reversed, however, no shortages are simulated because return flows from the upstream users are included in estimates of available supply to the downstream users.
Reservoirs and bifurcations
If reservoirs or bifurcations are present in the model, the algorithm can make additional reservoir releases or alter the distribution of flows through bifurcations to meet priority demands. Additional reservoir releases are only possible if a guide curve has been defined at the supplying reservoir with a lower priority than the downstream demand (see Guide Curve Level (for Global Ranking)). If more than one reservoir or bifurcation is available to meet a priority demand, then the supplying reservoir or bifurcation is determined based on 'model distance' rather than priority. The behavior of reservoirs and bifurcations is demonstrated with the following two examples, the first with two parallel reservoirs and the second with a bifurcation and a reservoir.
Reservoir example
In the example in Figure 11.2, water demands are the same as in the previous example. The system now includes two upstream reservoirs. Reservoir 1 and Reservoir 2 have guide curve levels defined and both guide curve levels have priorities that are lower than all three of the downstream demands. Therefore, both reservoirs can make releases to meet downstream demands. However, the distribution of downstream demands between the two reservoirs is determined by the principle of 'model distance', rather than the relative priorities of the two guide curve levels. The model distance is defined as the number of nodes between two model objects.
In the example, the global ranking algorithm will release 1 m^3/s from Reservoir 2, along with 1.5 m^3/s from Reservoir 1. Because the model distance from Water User 1 to Reservoir 2 is smaller than the distance to Reservoir 1, Water User 1's demand is met by releases from Reservoir 2. On the other hand, the demands at other two water use locations can only be met by Reservoir 1 due to water balance constraints.
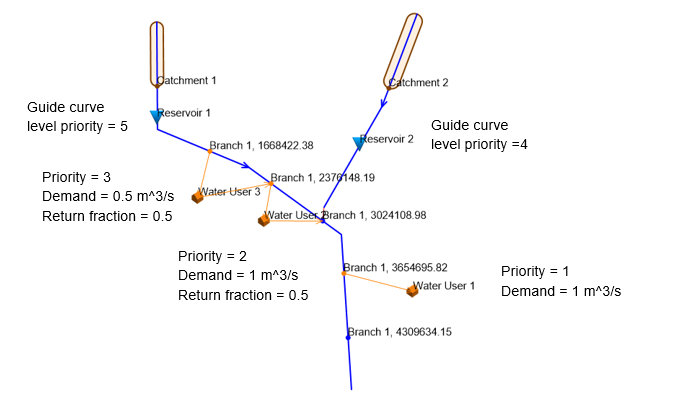
Because of the way that return flows are handled by the global ranking algorithm (see previous section), the total reservoir release from the two reservoirs (2.5 m^3/s), is higher than the net demand (1.75 m^3/s).
Bifurcation example
The global priority algorithm will also re-direct water away from bifurcations in order to meet priority demands. Let us consider bifurcation example in Figure 11.3. In the example, global ranking has not been applied. Therefore, the bifurcation routes flows away from the most downstream water user (Water User 1), resulting in a shortage. In the example, no releases are made from the upstream reservoir.
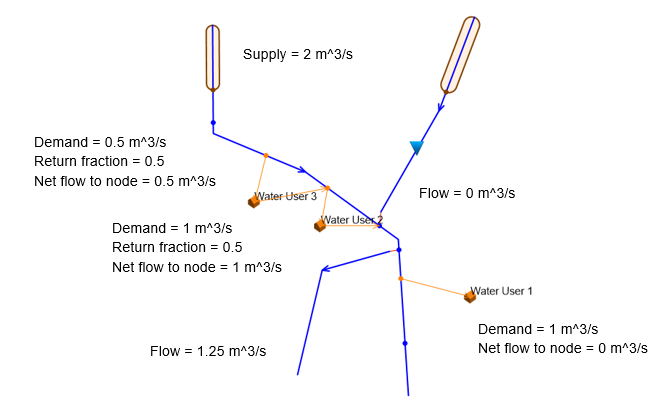
Figure 11.3 Bifurcation example before application of global ranking
After the application of global ranking, the ranking assigned to Water User 1 routes water away from the bifurcation in order to meet Water User 1's demand (Figure 11.4). Because the model distance to the bifurcation node is shorter than the model distance to the reservoir, Water User 1's demand is met by re-routing from the bifurcation rather than releasing from the reservoir.
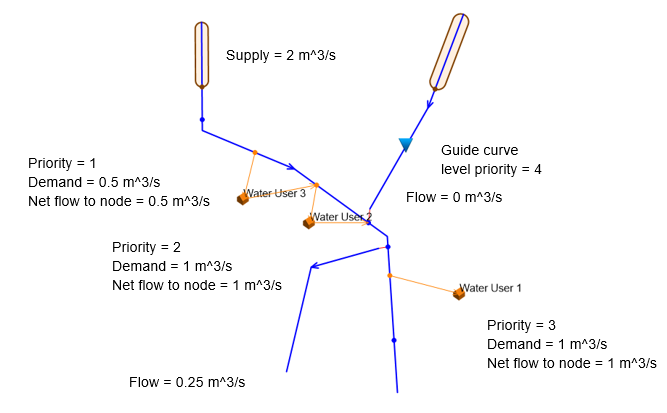
Figure 11.4 Bifurcation example after application of global ranking