Decay

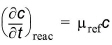
Biological degradation, radioactive decay or other kinds of attenuation of sol­utes can often be described as a first-order degradation process, with an exponential decrease of concentration over a half-life. This is described in MIKE SHE as

(34.11)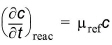   

where m_ref is the reference degradation rate coefficient calculated by

(34.12)   

where l is the half-life of the species.

Following the work of Boesten and van der Linden (1991), to overcome some of the difficulties in simplifying complex biological and chemical reactions, the decay in MIKE SHE is dependent of the soil moisture content and soil tem­perature as

(34.13)   

where the F_w is the water content function given as

(34.14)   

and where q is actual soil moisture, q_s is saturated moisture content and B is an empirical constant. F_t is the soil temperature function given as:

(34.15)   

(34.16)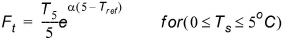   

(34.17)   

where T_s is the actual temperature of the soil, T_ref is the reference tempera­ture at which m_ref is measured and a is a constant depending on T, T_ref, the gas constant and the molar activation.

For simplicity the soil temperature over depth is calculated as a function of the air temperature by an experimentally derived formula given by Klein (1995)

(34.18)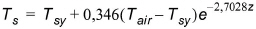   

where T_sy is the mean daily soil temperature from yesterday, T_air is the mean daily air temperature and z is depth.

Note that for large depths, this function responds very slowly to variations in air temperature. Therefore, long simulations may be necessary to achieve the required initial temperature distribution. An example of simulated soil temper­ature distributions as a function soil depth is shown in Figure 34.4.

MIKE SHE allows you to specify separate half-lives for the matrix and frac­tions in dual porosity models, since degradation is likely to be faster in the fractures where higher oxygen contents are more likely.

.

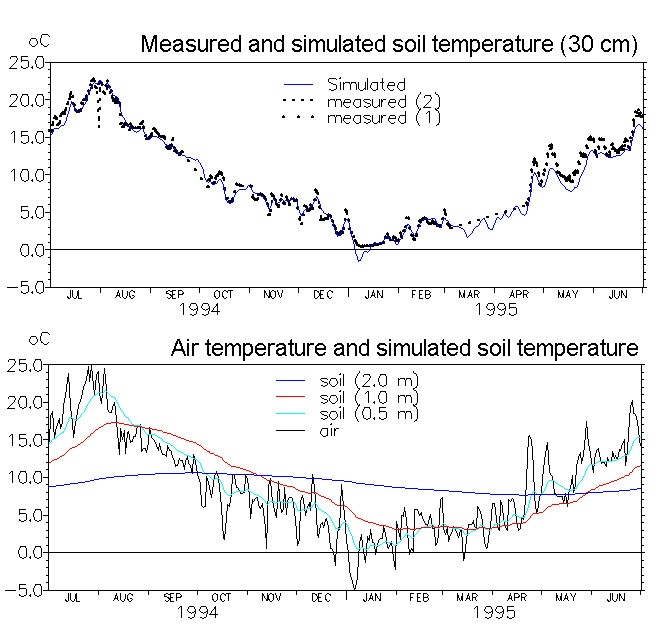
Figure 34.4        Application of the soil temperature function. Top: measured and simu­lated soil temperature in 30 cm depth (measurements were based on two replicates). Bottom: soil temperatures simulated in different depths based on measured air temperatures.