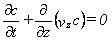
Solution Scheme

Similar to the saturated zone, the unsaturated solute transport is solved explicitly, using upstream differencing for the advection term and central dif­ferencing for the dispersion term.

Neglecting the dispersion terms and the source/sink term and assuming that the flow field satisfies the equation of continuity and varies uniformly within a grid cell, the advection component is

(33.22)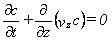   

:

Figure 33.5        Control volume defining an internal grid.

For the control volume shown in Figure 33.5, this equation is written in finite difference form as:

(33.23)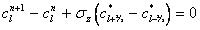   

where n denotes the time index, c_l is the concentration in the computational node, c* is the interpolated concentration at the edges of the grid at time n, and s_z is the directional Courant number defined by

(33.24)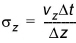   

As the c*-terms are not located at the nodal points, they have to be interpo­lated from known concentration values. The equation for this follows the one derived for the saturated zone

(33.25)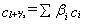   

However, in the unsaturated zone only three weights need to be determined

(33.26)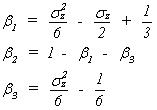   

where the weights are positioned relative to the actual flow direction.

Dispersive transport can be derived in a similar way. If the finite difference for­mulation of the dispersive transport is based on upstream differencing in con­centration and central differencing in the dispersion coefficients, the dispersive transport is

(33.27)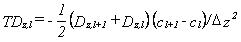   

The dispersive transport is incorporated into the weights.

The above solution is strictly speaking only valid for a regular discretisation but if the resolution varies slowly the error introduced is small.