Theoretical basis

Figure 24.8        Schematic of overland flow on a plane

Figure 24.8 represents a schematic of overland flow on a planar surface of infinite width with uniform rainfall. Precipitation falls on the plane, builds on the surface in response to the surface roughness, and flows down the slope in the positive x-direction. In the figure, L is the length of the slope, y is the local depth of water on the surface at any point along the surface and a is the slope. Then, from the continuity equation

(24.40)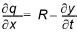   

where q is the specific discharge.

For turbulent flow on a plane of infinite width, the Manning equation is

(24.41)    [m²/s]

where M is the Mannings M.

Now, at equilibrium, the depth no longer changes and the specific discharge approaches the rainfall rate

(24.42)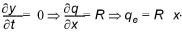   

where q_e is the equilibrium specific discharge.

Then, at equilibrium, the volume of water detained on the surface, D_e, can be calculated by

(24.43)    [m³/m]

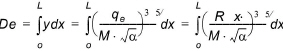
The depth, y, near the leading edge of the flow plane can be related to the depth at equilibrium by

(24.44)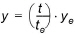    

where t is the time and t_e is the time until the equilibrium is reached.

Then from (24.41) we can write

(24.45)    [m²/s]

Now if we integrated the specific discharge from time 0 to when the equilib­rium is reached, we can calculate the total volume discharged, Q, (per unit width of the plane) by

(24.46)    [m²]

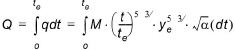
From (24.45), at equilibrium, (t = t_e), the depth of water at the leading edge of the plane (x = L) is

(24.47)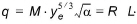   

which yields

(24.48) 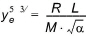  [m^5/3]

From continuity, the total volume of inflow up until equilibrium must equal the total outflow minus the amount retained on the surface. Thus,

Inflow - Outflow = Surface storage

which from equations (24.46) and (24.43) yields

(24.49)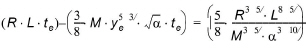   

which, when simplified, yields the time to reach equilibrium

(24.50)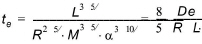   

If we now assume that the flow on the sloping plane is uniform, that is the change in discharge as a function of x is zero, then the depth prior to equilib­rium is simply

(24.51)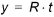   

and the relationship between the depth, y, and the surface storage at equilib­rium, D_e, is given by

(24.52)    [m]

The relationship between the depth, y, and the detained surface storage prior to equilibrium, D, is given by an empirical model (Fleming, 1975; Crawford and Linsley, 1966)

(24.53)    [m]

where during the recession part of the hydrograph, when D/D_e is greater than 1, D/D_e is assumed to be equal to 1.

Substituting (24.53) into the Manning equation (24.41) yields

(24.54)    [m²/s]