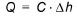
Groundwater exchange with MIKE Hydro River

The exchange flow, Q, between a saturated zone grid cell and the river link is calculated as a conductance, C, multiplied by the head difference between the river and the grid cell.

(27.1)   

Note that Eq. (27.1) is calculated twice - once for each cell on either side of the river link. This allows for different flow to either side of the river if there is a groundwater head gradient across the river, or if the aquifer properties are dif­ferent.

Referring to Figure 27.2, the head difference between a grid cell and the river is calculated as

(27.2)   

where h_grid is the head in the grid cell and h_riv is the head in the river link, as interpolated from the MIKE Hydro River h-points.

If the ground water level drops below the river bed elevation, the head differ­ence is calculated as

(27.3)   

where z_bot is the bottom of the simplified river link cross section, which is equal to the lowest point in the MIKE Hydro River cross-section.

In Eq. (27.1), the conductance, C, between the cell and the river link can depend on

·         the conductivity of the aquifer material only. See Aquifer Only Conduct­ance (V1 p. 532), or

·         the conductivity of the river bed material only. See River bed only con­ductance (V1 p. 533), or

·         the conductivity of both the river bed and the aquifer material. See Both aquifer and river bed conductance (V1 p. 534).

Aquifer Only Conductance

When the river is in full contact with the aquifer material, it is assumed that there is no low permeable lining of the river bed. The only head loss between the river and the grid node is that created by the flow from the grid node to the river itself. This is typical of gaining streams, or streams that are fast moving.

Thus, referring to Figure 27.2, the conductance, C, between the grid node and the river link is given by

(27.4)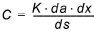   

where K is the horizontal hydraulic conductivity in the grid cell, da is the verti­cal surface available for exchange flow, dx is the grid size used in the SZ component, and ds is the average flow length. The average flow length, ds, is the distance from the grid node to the middle of the river bank in the triangu­lar, river-link cross-section. ds is limited to between 1/2 and 1/4 of a cell width, since the maximum river-link width is one cell width (half cell width per side).

There are three variations for calculating da:

·         If the water table is higher than the river water level, da is the saturated aquifer thickness above the bottom of the river bed. Note, however, that da is not limited by the bank elevation of the river cross-section, which means that if the water table in the cell is above the bank of the river, da accounts for overland seepage above the bank of the river.

·         If the water table is below the river level, then da is the depth of water in the river.

·         If the river cross-section crosses multiple model layers, then da (and therefore C) is limited by the available saturated thickness in each layer. The exchange with each layer is calculated independently, based on the da calculated for each layer. This makes the total exchange independent of the number of layers the river intersects.

This formulation for da assumes that the river-aquifer exchange is primarily via the river banks, which is consistent with the limitation that there is no unsaturated flow calculated beneath the river.

River bed only conductance

If there is a river bed lining, then there will be a head loss across the lining. In this case, the conductance is a function of both the aquifer conductivity and the conductivity of the river bed. However, when the head loss across the river bed is much greater than the head loss in the aquifer material, then the head loss in the aquifer can be ignored (e.g. if the bed material is thick and very fine and the aquifer material is coarse). This is the assumption used in many groundwater models, such as MODFLOW.

In this case, referring to Figure 27.2, the conductance, C, between the grid node and the river link is given by

(27.5)   

where dx is the grid size used in the SZ component, L_c is the leakage coeffi­cient [1/T] of the bed material, and w is the wetted perimeter of the cross-sec­tion.

In Eq. (27.5), the wetted perimeter, w, is assumed to be equal to the sum of the vertical and horizontal areas available for exchange flow. From Figure 27.2, this is equal to da + l_h, respectively. The horizontal infiltration length, l_h, is calculated based on the depth of water in the river and the geom­etry of the triangular river-link cross-section.

The infiltration area of the river link closely approximates the infiltration area of natural channels when the river is well connected to the aquifer. In this case, the majority of the groundwater-surface water exchange occurs through the banks of the river and decreases to zero towards the centre of the river. However, for losing streams separated from the groundwater table by an unsaturated zone, the majority of the infiltration occurs vertically and not through the river banks. In this case, the triangular shape of the river link does not really approximate wide losing streams.and the calculated infiltra­tion area may be too small - especially if the MIKE Hydro River bank eleva­tions are much higher than the river level. This can be compensated for by either choosing a lower bank elevation or by increasing the leakage coeffi­cient.

There are three variations for calculating da:

·         If the water table is higher than the river water level, da is the saturated aquifer thickness above the bottom of the river bed. Note, however, that da is not limited by the bank elevation of the river cross-section, which means that if the water table in the cell is above the bank of the river, da accounts for overland seepage above the bank of the river.

·         If the water table is below the river level, then da is the depth of water in the river.

·         If the river cross-section crosses multiple model layers, then da (and therefore C) is limited by the available saturated thickness in each layer. The exchange with each layer is calculated independently, based on the da calculated for each layer. This makes the total exchange independent of the number of layers the river intersects.

This formulation for da assumes that the river-aquifer exchange is primarily via the river banks, which is consistent with the limitation that there is no unsaturated flow calculated beneath the river.

Both aquifer and river bed conductance

If there is a river bed lining, then there will be a head loss across the lining. In this case, the conductance is a function of both the aquifer conductivity and the conductivity of the river bed and can be calculated as a serial connection of the individual conductances. Thus, referring to Figure 27.2, the conduct­ance, C, between the grid node and the river link is given by

(27.6)   

where K is the horizontal hydraulic conductivity in the grid cell, da is the verti­cal surface available for exchange flow, dx is the grid size used in the SZ component, ds is the average flow length, L_c is the leakage coefficient [1/T] of the bed material, and w is the wetted perimeter of the cross-section. The average flow length, ds, is the distance from the grid node to the middle of the river bank in the triangular, river-link cross-section. ds is limited to between 1/2 and 1/4 of a cell width, since the maximum river-link width is one cell width (half cell width per side).

In Eq. (27.5), the wetted perimeter, w, is assumed to be equal to the sum of the vertical and horizontal areas available for exchange flow. From Figure 27.2, this is equal to da + l_h, respectively. The horizontal infiltration length, l_h, is calculated based on the depth of water in the river and the geom­etry of the triangular river-link cross-section.

The infiltration area of the river link closely approximates the infiltration area of natural channels when the river is well connected to the aquifer. In this case, the majority of the groundwater-surface water exchange occurs through the banks of the river and decreases to zero towards the centre of the river. However, in the case of losing streams separated from the ground­water table by an unsaturated zone, the majority of the infiltration occurs ver­tically and not through the river banks. In this case, the horizontal infiltration area may be too small, if the MIKE Hydro River bank elevations are much higher than the river level. This can be compensated for by either choosing a lower bank elevation or by increasing the leakage coefficient.

·         There are three variations for calculating da:

·         If the water table is higher than the river water level, da is the saturated aquifer thickness above the bottom of the river bed. Note, however, that da is not limited by the bank elevation of the river cross-section, which means that if the water table in the cell is above the bank of the river, da accounts for overland seepage above the bank of the river.

·         If the water table is below the river level, then da is the depth of water in the river.

·         If the river cross-section crosses multiple model layers, then da (and therefore C) is limited by the available saturated thickness in each layer. The exchange with each layer is calculated independently, based on the da calculated for each layer. This makes the total exchange independent of the number of layers the river intersects.

This formulation for da assumes that the river-aquifer exchange is primarily via the river banks, which is consistent with the limitation that there is no unsaturated flow calculated beneath the river.