
The driving force for transport of water in the unsaturated zone is the gradient of the hydraulic head, h, which includes a gravitational component, z, and a pressure component, y. Thus,
The gravitational head at a point is the elevation of the point above the datum (z is positive upwards). The reference level for the pressure head component is the atmospheric pressure. Under unsaturated conditions the pressure head, y, is negative due to capillary forces and short range adsorptive forces between the water molecules and the soil matrix. These forces are responsible for the retention of water in the soil. As these two forces are difficult to separate, they are incorporated into the same term. Although the physical phenomena creating the pressure head under unsaturated and saturated conditions are very different, the pressure head is considered to be a continuous function across the water table, with the pressure being negative above and positive below the water table.
For vertical flow, the driving force for the transport of water is the vertical gradient of the hydraulic head. Thus,
(28.2) 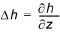
The volumetric flux is then obtained from Darcy's law:
where K(q) is the unsaturated hydraulic conductivity. Assuming that the soil matrix is incompressible and the soil water has a constant density, the continuity equation will be:
where q is the volumetric soil moisture and S is the root extraction sink term. Combining Eqs. (28.1), (28.3) and (28.4) yields
The dependent variables, q and y, in Eq. (28.5) are related through the hydraulic conductivity function, K(q), and the soil moisture retention curve, y(q)
Eq. (28.5) is general, in the sense that it is equally valid in both homogeneous and heterogeneous soil profiles, and there are no constraints on the hydraulic functions.
Introducing the concept of soil water capacity
(28.6) 
which is the slope on the soil moisture retention curve, then the tension-based version of Eq. (28.5) is
This equation is usually referred to as Richards equation, which is named after L.A. Richards who first used it in 1931. It still applies when y becomes positive, in which case the equation degenerates to the LaPlace equation.
The sink terms in Eq. (28.7) are calculated from the root extraction for the transpiration in the upper part of the unsaturated zone. The integral of the root extraction over the entire root zone depth equals the total actual evapotranspiration. Direct evaporation from the soil is calculated only for the first node below the ground surface.