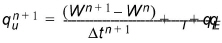
Steps in the Coupling Procedure

The following outlines the actual steps in the coupling procedure used for each UZ time step:

1.       If the total water content above the datum Zo (Zo should always be lower than the lowest elevation of the water table) is designated Wⁿ, the UZ contribution to the E_cum error term in UZ-time step n to n+1 is

(28.36)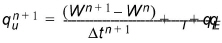   

where Wⁿ⁺¹ = the new water content; q_I = the infiltration rate (negative downwards); q_E = the evapotranspiration loss. (Note: negative values of qu indicate downward flow).

2.       Assuming that the groundwater outflow in a cell is steady, the accumu­lated error at UZ time n+1 is:

(28.37)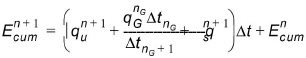   

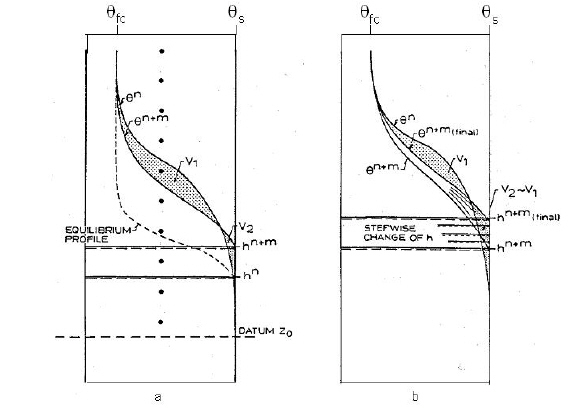
Figure 28.4        a) Soil moisture content at two times n and n+m without corrections, and b) Soil moisture content at time n+m before and after correction.

where 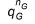 (positive outwards) is the sum of the groundwater outflow rate for the cell in the last groundwater time step (n_G) scaled to the new SZ time step length (n_G+1) and 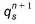(positive outwards) is the sum of source sink terms calculated by the UZ module for the current time n+1 (e.g., stream/aquifer exchanges, irrigation).

It should be noted that if E_cum is less than zero there is a deficit of water stored in the column and if E_cum is greater than zero there is an excess of water stored in the column.

3.       If 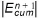 less than E_max corrections are not made for the current UZ time step.

4.       If 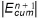 exceeds E_max the following corrections are made:

a) If 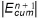is negative or positive, the water table is raised or low­ered, respectively, in prescribed increments that depend on the dis­tance between UZ nodes and the UZ-calculation in time step n to n+1 is repeated as described above.

b) In the Full Richards solution the UZ flow solution is repeated for the last three nodes above the water table to reduce numerical overhead. In the Gravity Flow option, the UZ flow solution is repeated for the entire column. The UZ flow solution is not repeated for the two-layer UZ option.

c) The change in water volume W^n+1* over the entire column is com­puted and a new 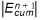is calculated.

d) If 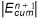 is less than a^.E_max, where a is a hard-coded correction factor equal to 0.9, the error associated with the solution is consid­ered acceptable and the procedure stops. If  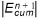is greater than or equal to a^.E_max, the solution is unacceptable and steps a) through d) are repeated until criteria d) is satisfied. The value a defines a threshold for stopping the procedure lower than that used to initiate the procedure, which prevents correction overshoots.

e) If 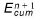 changes sign the solution is considered acceptable and the procedure stops. The adjustment required to obtain a  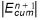value of zero is calculated using a secant line approach.

5.       A new recharge rate, 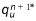 is calculated taking the adjustments into account.

(28.38)   

where h^n* is the new water table elevation after step d) calculated by the UZ module and Dt is the length of the current UZ time step (n+1). If SZ outflows for the next SZ time step (n_G+1) are unchanged, the water table from the SZ calculation will be hⁿ⁺¹ = h^n* calculated in the last UZ time step before an SZ time step (see Eq. (28.38)).

If 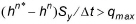, where q_max, is a maximum infiltration rate, the corrected rate is reduced to q_max. In the Richards Equation and Gravity Flow options q_max is 0.7K_s and 0.4K_s for rising and falling water table conditions, respectively, where K_s is the saturated hydraulic con­ductivity of the UZ node at the water table. In the Two-layer UZ option, the infiltration rate is used to constrain the corrected rate.

Steps 1-5 are repeated for all UZ time steps within each SZ time step. The flows are accumulated and passed as an average rate, q_u, for the next SZ time step. The average q_u is used as a flux boundary condition in the SZ dif­ferential equations.