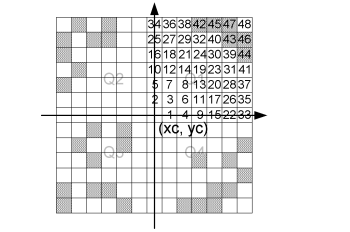
This technique finds four points from the raw data set - one in each quadrant. The search is done in the following way. A mask of relative indices is created. The cells in this mask are sorted according to the distance. For the quadrant Q1 the cells are sorted in the following way, the grid point it self being excluded.

Figure 10.2 Illustration of the neighbouring grid cells being sorted
Note that the grid cells with a crosshatch pattern contain raw data points. When the closest raw data point in each quadrant is found, we have four points that form a quadrangle. This quadrangle contains the centre point, where we want to calculate the z-value. This is illustrated on Figure 10.3.
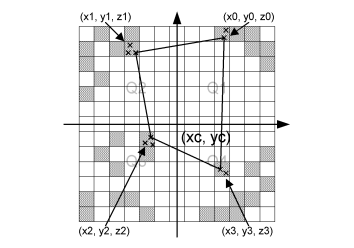
Figure 10.3 Illustration of the closest raw data points in each quadrant.
Note that each grid cell might contain more raw data points. If this is the case, the closest of these is chosen. We now have an irregular quadrangle, where the elevation is defined in each vertex. We need to compute the elevation in (xc, yc). If we transform our quadrangle into a square, we can perform bilinear interpolation. This is illustrated on Figure 10.4.
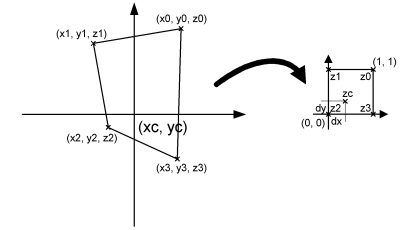
Figure 10.4 Illustration of bilinear interpolation.
First the interpolation requires the transformation from quadrangle to a normalized square. This is done in the by computing 8 coefficients in the following way:
(10.1) 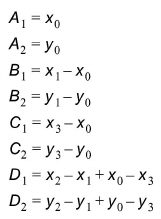
Mapping the coordinates (xc, yc) to the normalized square (dx, dy) is done by solving equation (10.2).
where the coefficients are
(10.3) 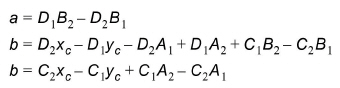
Solving equation (10.2) gives us dx.
(10.4) 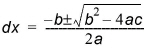
where 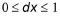 is used to choose the correct root. dy can now be computed in two ways:
is used to choose the correct root. dy can now be computed in two ways:
or
Choosing between (10.5) and (10.6) is done in such a way, that division by zero is avoided. (xc, yc) has been mapped to (dx, dy). The task was to compute the elevation in the point (xc, yc) and this is done in the following way using regular bilinear interpolation:
(10.7) 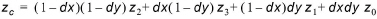
If less than four points are found (if one or more quadrants are empty), the double linear interpolation is replaced with reverse distance interpolation (RDI). This is done according to the following scheme:
(10.8) 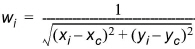
(10.9) 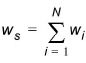
(10.10) 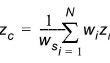
The method works fairly efficiently, but it has one drawback. The quadrant search is heavily dependent on the orientation of the bathymetry. If the bathymetry is rotated 45 degrees 4 completely different points might be used for the interpolation. For this reason there is also a Triangular interpolation method, which can be used, and this method should be direction independent.