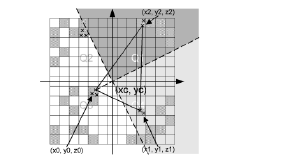
As mentioned previously the ‘Bilinear Interpolation’ is dependent on the orientation of the bathymetry. The ‘Triangular Interpolation’ is made as an answer to this problem. First the closest point to (xc, yc) is found. The following figure shows this:

Figure 10.5 Illustration of triangular interpolation
In this example the point (x0, y0, z0) is the closest point. When this point is identified, two quadrants are identified – indicated by the light grey and the dark grey areas. The closest point in these two quadrants are then found. They can be seen on the figure as (x1, y1, z1) and (x2, y2, z2). The interpolation is then done in two steps. First the coefficients describing the plane defined by the 3 found points are computed:
(10.11) 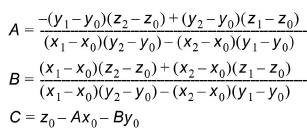
And secondly the actual interpolation is done:
(10.12) 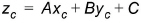
If less than 3 points are found, reverse distance interpolation (RDI) is used. The triangular interpolation is more time consuming due to the more complex direction independent search, but better end results should be achieved with this method.