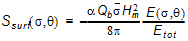
Depth-induced breaking occurs when waves propagate into very shallow areas, and the wave height can no longer be supported by the water depth. The formulation of wave breaking is based on the breaking model by Battjes and Janssen (1978). Eldeberky and Battjes (1995) proposed a spectral version of the breaking model, where the spectral shape was no influenced by breaking.
The source term due to depth-induced breaking can be written
(6.9)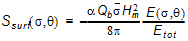
where a ยป 1.0 is a calibration constant, Qb is the fraction of breaking waves,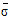 
is the mean relative frequency, Etot is the total wave energy and 
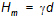is the maximum wave height. Here g is the free breaking parameter (a wave height - to depth ratio).
Based on laboratory data and field data it has been shown that the breaking parameter g varies significantly depending on the wave conditions and the bathymetry. Kaminsky and Kraus (1993) found that g values in the range between 0.6 and 1.59 with an average of 0.79. A number of expressions for determination of the breaking parameter g have been proposed in literature. Battjes and Stive (1985) found that g depends weakly on the deep water wave steepness. They proposed the following expression
(6.10)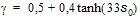 
Here s0 = H0 /L0 is the deep water steepness, where H0 and L0 is the wave height and the wave length, respectively, in deep water. This formulation can not be used in the present spectral wave model, because the value of g is not determined based on local parameters. Nelson (1987, 1994) found that g can be determined as a function of the local bottom slope,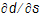 
, in the mean wave direction. Nelson suggested the following expression
(6.11)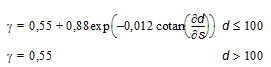 
Recently, Ruessink et al. (2003) have presented a new empirical form for g, where g is determined as a function of the product of the local wave number k and the water depth d
(6.12) 
Ruessink et al. showed that using this formulation for the breaking parameter the prediction of the wave heights in the breaking zone can be improved for barred beaches. However, the new formulation is also applicable to planar beaches.
