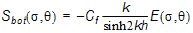
As waves propagate into shallow water, the orbital wave velocities penetrate the water depth and the source terms due to wave-bottom interaction become important. Furthermore, the deep-water source terms are modified because of depth effects. A review of the different wave-bottom interaction processes is given by Shemdin et al. (1978), who consider dissipation due to friction in the turbulent boundary layer, percolation into a porous bottom, motion of a soft bottom and scattering on bottom irregularities. According to Shemdin et al. (1978) bottom friction is generally dominant when the sediment is composed of fine sand, d50 = 0.1-0.4 mm or when sand ripples are present. In this case, the low permeability prohibits percolation and granular friction prevents viscous flow behaviour (Shemdin et al., 1978). In many practical cases, the bed is composed of fine sand or wave-generated ripples are present (e.g. Dingler and Inman (1976) found this to be true on many continental shelves).
For the fully spectral formulation the bottom dissipation source function is based on linear theory and can be generalised into Eq. (6.13) below, Weber (1991)
where Cf is a dissipation coefficient (= fwUbm), which depends on the hydrodynamic and sediment conditions. Here fw is the wave friction factor and Ubm is the maximum near-bed particle velocity given by
(6.14) 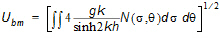
Further details are described in Johnson and Kofoed-Hansen (2000).