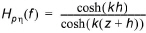
In the Transfer Functions dialog you specify the name and define one or more filter components. All filter components (transfer functions) are defined in the frequency domain. Already defined transfer function can be temporarily excluded from the analysis by setting the number of transfer functions to include.
The available basic transfer functions and parameters are listed below.
The transfer function for a low-pass filter suppresses all frequency components of the time series above the cut-off frequency.
The transfer function for a high-pass filter suppresses all frequency components of the time series below the cut-off frequency.
The transfer function for a band-pass filter lets all frequency components of the time series between the lower and higher cut-off frequencies pass.
The transfer function of a band-stop filter suppresses all frequency components of the time series between the lower and higher cut-off frequencies.
The transfer function for a differentiation filter differentiates the input time series to a given order.
The transfer function for an integration filter integrates the input time series to a given order.
The transfer function for a notch filter suppresses a specific frequency component of the time series.
The transfer function for a pressure to surface elevation filter attenuates all frequency components of a pressure time series to an equivalent time series of surface elevation.
(4.1) 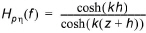
in which z is the distance from still water level to the pressure sensor (must be negative). As the transfer function increases rapidly with frequency and potentially causes a dramatic amplification of measurement noise a maximum amplification factor may be given. The wave number k is given by the dispersion relation:
(4.2) 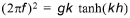
The above definition are based on linear wave theory.
The transfer function for a moving average filter defines an equivalent weighting of the time series data within the period.
The transfer function for a Biesel (piston) filter attenuates all frequency components of a piston position time series for a piston type wave maker (with zero deviation) to an equivalent time series of surface elevation (Biésel, 1951).
(4.3) 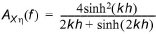
The transfer function for an evanescent mode (piston) filter produces the frequency dependent local disturbance due to a varying piston position of a piston type wave maker (with zero deviation) (Schäffer et. al., 1994).
(4.4) 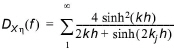
where kj is an evanescent-mode wave number given by the j'th solution to:
(4.5) 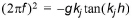
The transfer function for a Bartlett or triangular filter yields a low-pass filter for which the attenuation above the cut-off frequency smoothly decreases towards zero.
The transfer function for the elevation to pressure filter attenuates all frequency components of a surface elevation time series to an equivalent time series of pressure.
(4.6) 
In which z is the distance from still water level to the level at which the pressure should be calculated (must be negative and not exceed the water depth). The wave number k is given by the dispersion relation.
(4.7) 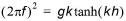
The above definitions are based on linear wave theory.
The transfer function of a filter for displacement of a surface elevation a certain distance in the propagation direction produces a phase shift of all frequency components (no attenuation occurs).
(4.8) 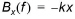
In which x is the displacement in the propagation direction (can be negative). The wave number k is given by the dispersion relation.
(4.9) 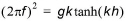
The above definitions are based on linear wave theory.
The filter transfer function is specified in terms of basic transfer functions which may be superposed. One example is the conversion of time series data from a pressure sensor located at the sea bottom to an equivalent time series of surface elevations. This operation can be performed swiftly by combining the transfer function for pressure to surface elevation with a high-pass filter. The latter automatically removes tidal variations and subtracts the still water level.