Successive Over-Relaxation (SOR) Numerical Solution
The method for solving the overland flow equations is similar to the method applied to the saturated zone flow. A linear matrix system of N equations with N unknown water levels is derived. The matrix is then solved iteratively, using the modified Gauss Seidel method. Because of the non-linear relationship between water levels and flows, the 2nd order term is included in the Taylor series expressing the correction of water levels as a function of the residuals.
The flow is calculated for the remainder of any iteration using Eq. (24.13) whenever there is sufficient water in a cell, that is, whenever hu exceeds the minimum threshold that is specified by the user.
The exchange between ponded water and the other hydrologic components (e.g. direct exchange with the saturated zone, unsaturated infiltration, and evaporation) is added or subtracted from the amount of ponded water in the cell at the beginning of every overland flow time step.
As the flow equations, so to speak, are explicit during one iteration, it is necessary to reduce the calculated flows in some situations to avoid internal water balance errors and divergence of the solution scheme.
Thus, requiring that the water depth cannot be negative, which implies that Dh ³ -h(t), rearranging Eq. (24.11) gives:
(24.14) 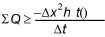
where SQ is the sum of outflows and inflows.
Splitting SQ into inflows and outflows and remembering that outflow is negative, gives:
remembering that I = iDx2 and i is the net input into overland flow (net rainfall less infiltration).
If necessary during an iteration, these calculated outflows are reduced to satisfy the equal sign of (24.15).
To ensure that the inflows, SQin, have been summed before calculating SQout, the grid squares are treated in order of descending ground levels during each iteration.