Upper boundary

The upper boundary condition is either

·         a constant flux condition within each time step (Neumann boundary con­dition), which is determined by the infiltration rate, or

·         a constant head condition within each time step (Dirichlet boundary con­dition), which is determined by the level of ponded water on the surface.

If the infiltration is equal to the net rainfall rate at the soil surface, R, Eq. (28.9) can be written for the top node N as

(28.20)       

where R is defined negative downwards.

Writing Eq. (28.20) in a similar form to Eq. (28.12) yields

(28.21)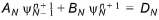      

where

(28.22)      

If water is ponded on the ground surface, the first node is assumed saturated and the boundary condition simply becomes

(28.23)      

At the beginning of each UZ time step, the amount of available water for infil­tration is calculated as the amount of ponded water, plus the net rainfall at the ground surface, minus evaporation from ponded water.

The upper boundary condition is applied depending on the deficit in the uppermost UZ node:

·         If the available water exceeds the deficit in the top UZ node, then the head boundary is used.

·         If the available water is less then the deficit in the top UZ node, then a flux boundary is used.

If the head boundary is used, then when the solution is found, the amount of infiltration is compared against the available amount of infiltration. If the avail­able infiltration is exceeded then the solution is repeated with the flux bound­ary.

If the flux boundary is used, then the available water for infiltration is divided by the time step length to get the infiltration rate. When the solution is found, the water content in the uppermost UZ node is compared to the saturated water content. If the saturated water content was reached or exceeded, then the solution is repeated using the head boundary.

The solution is restricted to a maximum of one repeat in each time step, to prevent an infinite loop.